| Next Page | Up One Level |
Lecture Slides available: PDF PowerPoint
Relational Algebra
Contents
- Terminology
- Operators - Write
- Operators - Retrieval
- Relational SELECT
- Relational PROJECT
- SELECT and PROJECT
- Set Operations - semantics
- SET Operations - requirements
- UNION Example
- INTERSECTION Example
- DIFFERENCE Example
- CARTESIAN PRODUCT
- CARTESIAN PRODUCT example
- JOIN Operator
- JOIN Example
- Natural Join
- OUTER JOINs
- OUTER JOIN example 1
- OUTER JOIN example 2
In order to implement a DBMS, there must exist a set of rules which state how the database system will behave. For instance, somewhere in the DBMS must be a set of statements which indicate than when someone inserts data into a row of a relation, it has the effect which the user expects. One way to specify this is to use words to write an `essay' as to how the DBMS will operate, but words tend to be imprecise and open to interpretation. Instead, relational databases are more usually defined using Relational Algebra.
Relational Algebra is :
- the formal description of how a relational database operates
- an interface to the data stored in the database itself
- the mathematics which underpin SQL operations
Operators in relational algebra are not necessarily the same as SQL operators, even if they have the same name. For example, the SELECT statement exists in SQL, and also exists in relational algebra. These two uses of SELECT are not the same. The DBMS must take whatever SQL statements the user types in and translate them into relational algebra operations before applying them to the database.
Terminology
- Relation - a set of tuples.
- Tuple - a collection of attributes which describe some real world entity.
- Attribute - a real world role played by a named domain.
- Domain - a set of atomic values.
- Set - a mathematical definition for a collection of objects which contains no duplicates.
Operators - Write
- INSERT - provides a list of attribute values for a new tuple in a relation. This operator is the same as SQL.
- DELETE - provides a condition on the attributes of a relation to determine which tuple(s) to remove from the relation. This operator is the same as SQL.
- MODIFY - changes the values of one or more attributes in one or more tuples of a relation, as identified by a condition operating on the attributes of the relation. This is equivalent to SQL UPDATE.
Operators - Retrieval
There are two groups of operations:
- Mathematical set theory based relations:
UNION, INTERSECTION, DIFFERENCE, and CARTESIAN PRODUCT. - Special database operations:
SELECT (not the same as SQL SELECT), PROJECT, and JOIN.
Relational SELECT
SELECT is used to obtain a subset of the tuples of a relation that satisfy a select condition.
For example, find all employees born after 1st Jan 1950:
SELECTdob '01/JAN/1950'(employee)
Relational PROJECT
The PROJECT operation is used to select a subset of the attributes of a relation by specifying the names of the required attributes.
For example, to get a list of all employees surnames and employee numbers:
PROJECTsurname,empno(employee)
SELECT and PROJECT
SELECT and PROJECT can be combined together. For example, to get a list of employee numbers for employees in department number 1:
-

- Figure : Mapping select and project
Set Operations - semantics
Consider two relations R and S.
- UNION of R and S
the union of two relations is a relation that includes all the tuples that are either in R or in S or in both R and S. Duplicate tuples are eliminated. - INTERSECTION of R and S
the intersection of R and S is a relation that includes all tuples that are both in R and S. - DIFFERENCE of R and S
the difference of R and S is the relation that contains all the tuples that are in R but that are not in S.
SET Operations - requirements
For set operations to function correctly the relations R and S must be union compatible. Two relations are union compatible if
- they have the same number of attributes
- the domain of each attribute in column order is the same in both R and S.
UNION Example
-

- Figure : UNION
INTERSECTION Example
-
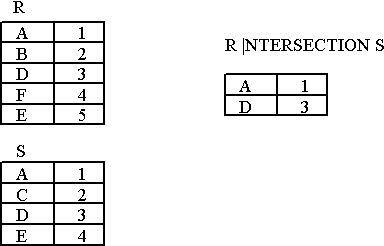
- Figure : Intersection
DIFFERENCE Example
-
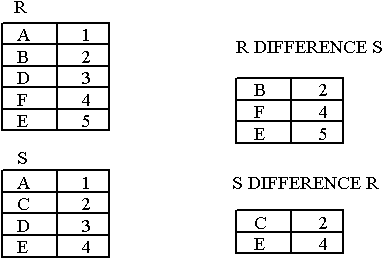
- Figure : DIFFERENCE
CARTESIAN PRODUCT
The Cartesian Product is also an operator which works on two sets. It is sometimes called the CROSS PRODUCT or CROSS JOIN.
It combines the tuples of one relation with all the tuples of the other relation.
CARTESIAN PRODUCT example
-
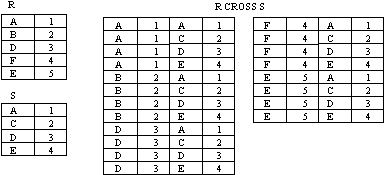
- Figure : CARTESIAN PRODUCT
JOIN Operator
JOIN is used to combine related tuples from two relations:
- In its simplest form the JOIN operator is just the cross product of the two relations.
- As the join becomes more complex, tuples are removed within the cross product to make the result of the join more meaningful.
- JOIN allows you to evaluate a join condition between the attributes of the relations on which the join is undertaken.
The notation used is
R JOINjoin condition S
JOIN Example
-
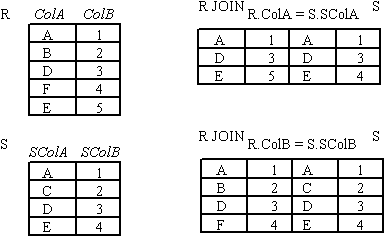
- Figure : JOIN
Natural Join
Invariably the JOIN involves an equality test, and thus is often described as an equi-join. Such joins result in two attributes in the resulting relation having exactly the same value. A `natural join' will remove the duplicate attribute(s).
- In most systems a natural join will require that the attributes have the same name to identify the attribute(s) to be used in the join. This may require a renaming mechanism.
- If you do use natural joins make sure that the relations do not have two attributes with the same name by accident.
OUTER JOINs
Notice that much of the data is lost when applying a join to two relations. In some cases this lost data might hold useful information. An outer join retains the information that would have been lost from the tables, replacing missing data with nulls.
There are three forms of the outer join, depending on which data is to be kept.
- LEFT OUTER JOIN - keep data from the left-hand table
- RIGHT OUTER JOIN - keep data from the right-hand table
- FULL OUTER JOIN - keep data from both tables
OUTER JOIN example 1
-
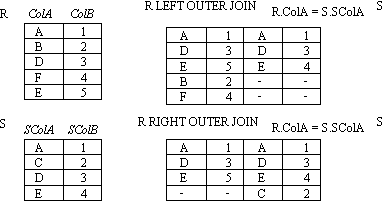
- Figure : OUTER JOIN (left/right)
OUTER JOIN example 2
-
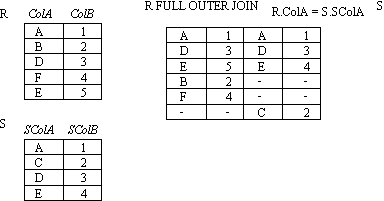
- Figure : OUTER JOIN (full)
| Next Page | Up One Level |
| ||||
| ||||
|